Exploratory Data Analysis

Setup

# Save packages as a vector
all.lib<-c("tidyverse","ggplot2", "dplyr","tidyr","modelr")

# Load packages
lapply(all.lib,require,character.only=TRUE)

Introduction:

Steps to exploratory data analysis:

Generate questions and hypothesis about the data.
Understand your data
Read the metadata if the data is not yours
Think about the analysis plan led by questions
Make sure your hypothesis-driven studies are clearly stated

Load your data: Example 1

a. Fuel economy data from 1999 to 2008 for 38 popular models of cars. The subset dataset from EPA. Full data available [here](https://fueleconomy.gov). A dataframe with 234 rows and 11 variables:

Variable
manufacturer	manufacturer name
model	model name
displ	engine displacement, in liters
year	year of manufacturer
cyl	number of cylinders
trans	type of transmission
drv	type of drive train, front wheel, rear wheel
cty	city miles per gallon
hwy	highway miles per gallon
fl	fuel type
class	“type” of car

# Load data
data("mpg")
head(mpg)

# A tibble: 6 × 11
  manufacturer model displ  year   cyl trans      drv     cty   hwy fl    class 
  <chr>        <chr> <dbl> <int> <int> <chr>      <chr> <int> <int> <chr> <chr> 
1 audi         a4      1.8  1999     4 auto(l5)   f        18    29 p     compa…
2 audi         a4      1.8  1999     4 manual(m5) f        21    29 p     compa…
3 audi         a4      2    2008     4 manual(m6) f        20    31 p     compa…
4 audi         a4      2    2008     4 auto(av)   f        21    30 p     compa…
5 audi         a4      2.8  1999     6 auto(l5)   f        16    26 p     compa…
6 audi         a4      2.8  1999     6 manual(m5) f        18    26 p     compa…

Exploring the data

# Useful functions in exploring the data
tail(mpg)

# A tibble: 6 × 11
  manufacturer model  displ  year   cyl trans      drv     cty   hwy fl    class
  <chr>        <chr>  <dbl> <int> <int> <chr>      <chr> <int> <int> <chr> <chr>
1 volkswagen   passat   1.8  1999     4 auto(l5)   f        18    29 p     mids…
2 volkswagen   passat   2    2008     4 auto(s6)   f        19    28 p     mids…
3 volkswagen   passat   2    2008     4 manual(m6) f        21    29 p     mids…
4 volkswagen   passat   2.8  1999     6 auto(l5)   f        16    26 p     mids…
5 volkswagen   passat   2.8  1999     6 manual(m5) f        18    26 p     mids…
6 volkswagen   passat   3.6  2008     6 auto(s6)   f        17    26 p     mids…

ncol(mpg)

[1] 11

nrow(mpg)

[1] 234

dim(mpg)

[1] 234  11

str(mpg)

tibble [234 × 11] (S3: tbl_df/tbl/data.frame)
 $ manufacturer: chr [1:234] "audi" "audi" "audi" "audi" ...
 $ model       : chr [1:234] "a4" "a4" "a4" "a4" ...
 $ displ       : num [1:234] 1.8 1.8 2 2 2.8 2.8 3.1 1.8 1.8 2 ...
 $ year        : int [1:234] 1999 1999 2008 2008 1999 1999 2008 1999 1999 2008 ...
 $ cyl         : int [1:234] 4 4 4 4 6 6 6 4 4 4 ...
 $ trans       : chr [1:234] "auto(l5)" "manual(m5)" "manual(m6)" "auto(av)" ...
 $ drv         : chr [1:234] "f" "f" "f" "f" ...
 $ cty         : int [1:234] 18 21 20 21 16 18 18 18 16 20 ...
 $ hwy         : int [1:234] 29 29 31 30 26 26 27 26 25 28 ...
 $ fl          : chr [1:234] "p" "p" "p" "p" ...
 $ class       : chr [1:234] "compact" "compact" "compact" "compact" ...

summary(mpg)

 manufacturer          model               displ            year     
 Length:234         Length:234         Min.   :1.600   Min.   :1999  
 Class :character   Class :character   1st Qu.:2.400   1st Qu.:1999  
 Mode  :character   Mode  :character   Median :3.300   Median :2004  
                                       Mean   :3.472   Mean   :2004  
                                       3rd Qu.:4.600   3rd Qu.:2008  
                                       Max.   :7.000   Max.   :2008  
      cyl           trans               drv                 cty       
 Min.   :4.000   Length:234         Length:234         Min.   : 9.00  
 1st Qu.:4.000   Class :character   Class :character   1st Qu.:14.00  
 Median :6.000   Mode  :character   Mode  :character   Median :17.00  
 Mean   :5.889                                         Mean   :16.86  
 3rd Qu.:8.000                                         3rd Qu.:19.00  
 Max.   :8.000                                         Max.   :35.00  
      hwy             fl               class          
 Min.   :12.00   Length:234         Length:234        
 1st Qu.:18.00   Class :character   Class :character  
 Median :24.00   Mode  :character   Mode  :character  
 Mean   :23.44                                        
 3rd Qu.:27.00                                        
 Max.   :44.00

Creating a tibble

data <- data.frame(a = 1:3, b = letters[1:3], c = Sys.Date() - 1:3)

data

  a b          c
1 1 a 2024-04-24
2 2 b 2024-04-23
3 3 c 2024-04-22

#>   a b          c
#> 1 1 a 2023-02-21
#> 2 2 b 2023-02-20
#> 3 3 c 2023-02-19

as_tibble(data)

# A tibble: 3 × 3
      a b     c         
  <int> <chr> <date>    
1     1 a     2024-04-24
2     2 b     2024-04-23
3     3 c     2024-04-22

#> # A tibble: 3 × 3
#>       a b     c         
#>   <int> <chr> <date>    
#> 1     1 a     2023-02-21
#> 2     2 b     2023-02-20
#> 3     3 c     2023-02-19

## Creating a tibble from preloaded dataset
data(iris)
head(iris)

  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa

as_tibble(iris)

# A tibble: 150 × 5
   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
          <dbl>       <dbl>        <dbl>       <dbl> <fct>  
 1          5.1         3.5          1.4         0.2 setosa 
 2          4.9         3            1.4         0.2 setosa 
 3          4.7         3.2          1.3         0.2 setosa 
 4          4.6         3.1          1.5         0.2 setosa 
 5          5           3.6          1.4         0.2 setosa 
 6          5.4         3.9          1.7         0.4 setosa 
 7          4.6         3.4          1.4         0.3 setosa 
 8          5           3.4          1.5         0.2 setosa 
 9          4.4         2.9          1.4         0.2 setosa 
10          4.9         3.1          1.5         0.1 setosa 
# ℹ 140 more rows

# Saving the tibble a new dataset
iris.updated<-as_tibble(iris)

1. Finding patterns in data through visualization and transformations

Categorical variable

Using geom_bar for displaying categorical variable,

ggplot(data = mpg) +
  geom_bar(mapping = aes(x = manufacturer))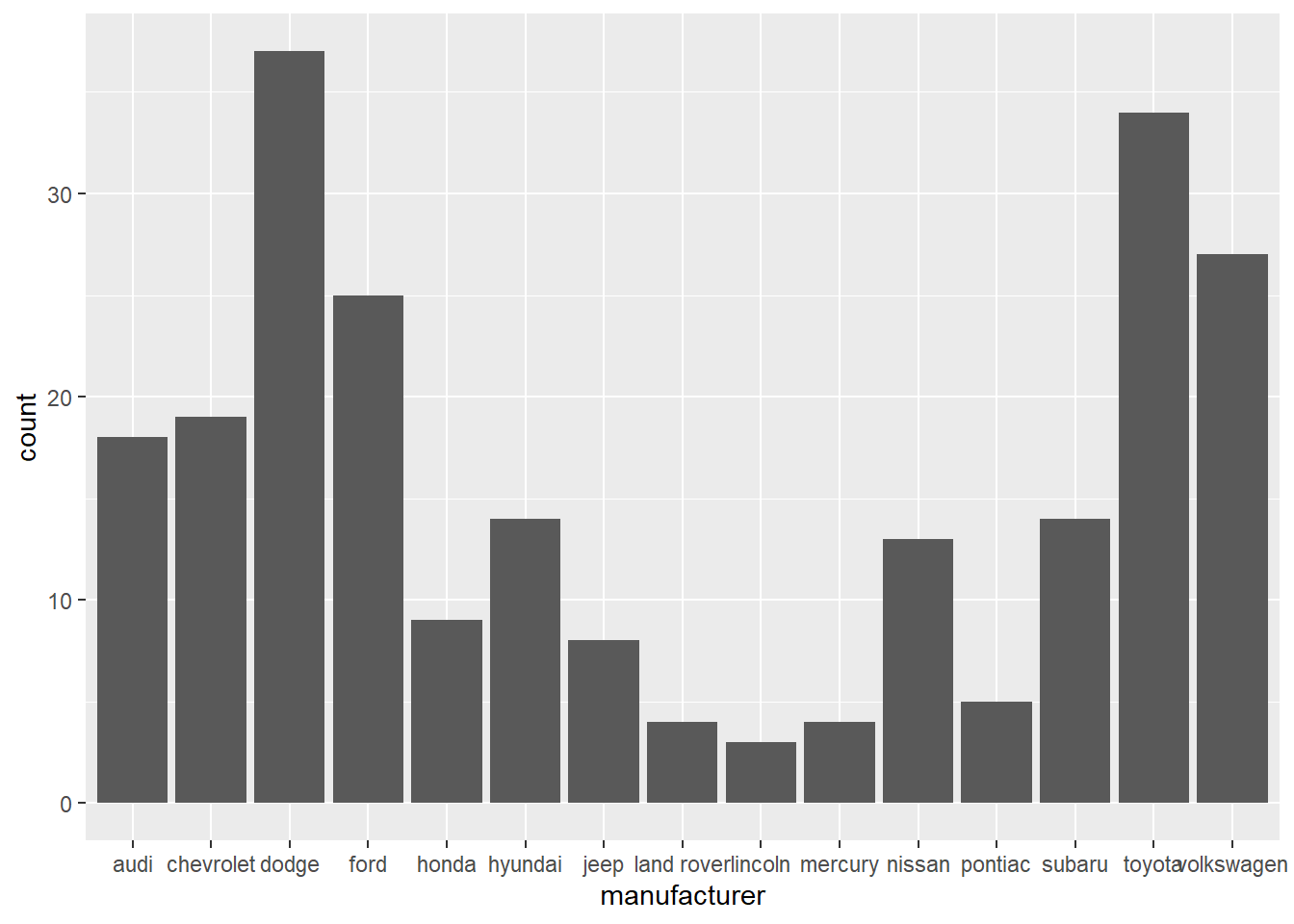

**Figure** 1. Displaying categorical variable with mpg.

Using the same above example for iris dataset, using the categorical variable,

ggplot(data = iris) +
  geom_bar(mapping = aes(x = Species))

**Figure** 2. Displaying categorical variable with iris.

Notice how the bars are equal because the y axis that shows the count is same (i.e 50) for each of the species.

Count function

The height of the bars displays how many observations occurred with each x value.

mpg %>% 
  count(manufacturer)

# A tibble: 15 × 2
   manufacturer     n
   <chr>        <int>
 1 audi            18
 2 chevrolet       19
 3 dodge           37
 4 ford            25
 5 honda            9
 6 hyundai         14
 7 jeep             8
 8 land rover       4
 9 lincoln          3
10 mercury          4
11 nissan          13
12 pontiac          5
13 subaru          14
14 toyota          34
15 volkswagen      27

Continuous variable

Using geom_bar for a continuous variable,

Note: geom_bar() makes the height of the bar proportional to the number of cases in each group

mpg %>%
 ggplot()+
 geom_bar(mapping = aes(x = displ), binwidth = 0.5)

Warning in geom_bar(mapping = aes(x = displ), binwidth = 0.5): Ignoring unknown
parameters: `binwidth`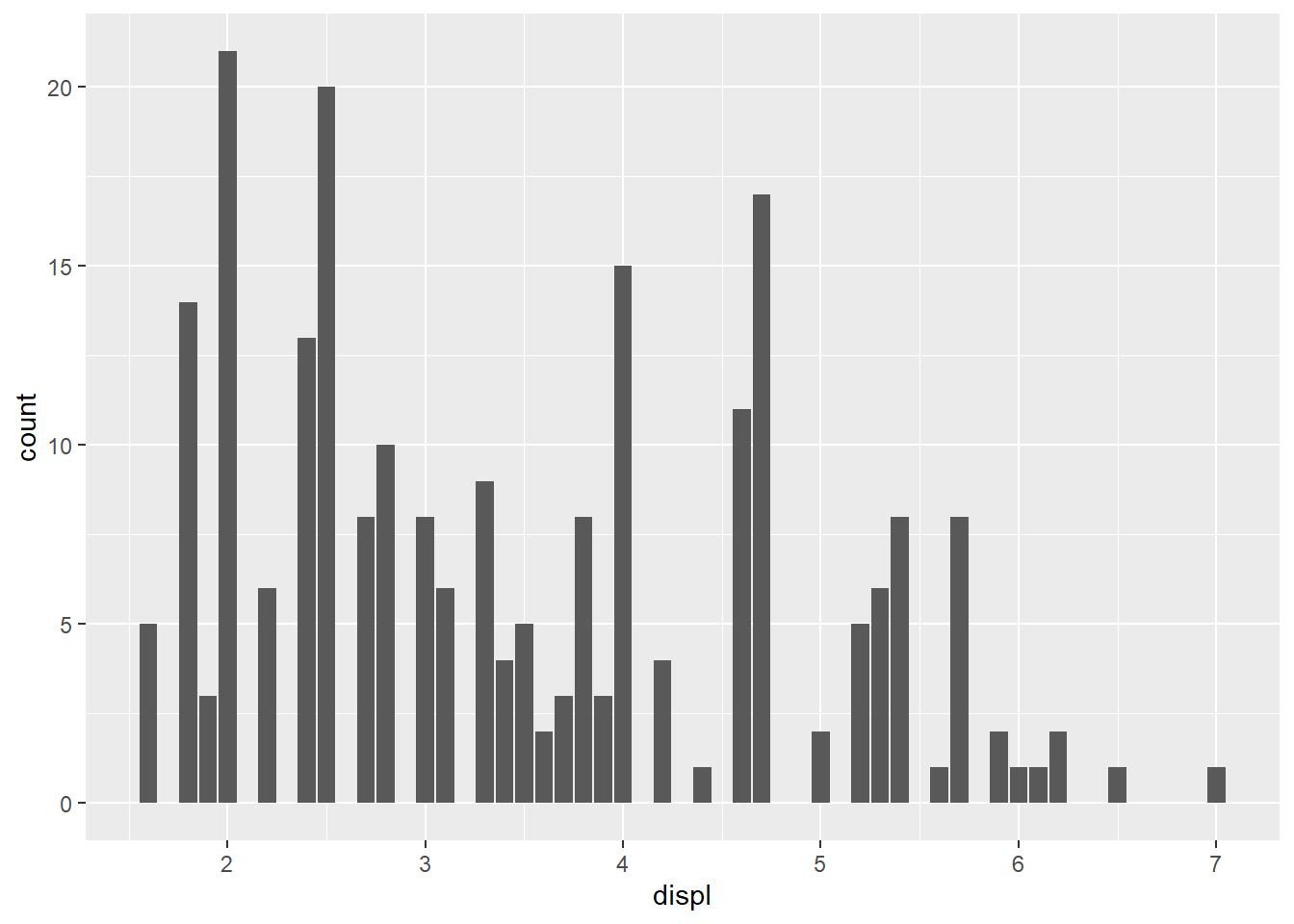

**Figure** 3. Displaying continuous variable with mpg.

Using histogram for continuous variable,

mpg %>%
 ggplot()+
 geom_histogram(mapping = aes(x = displ), binwidth = 0.5)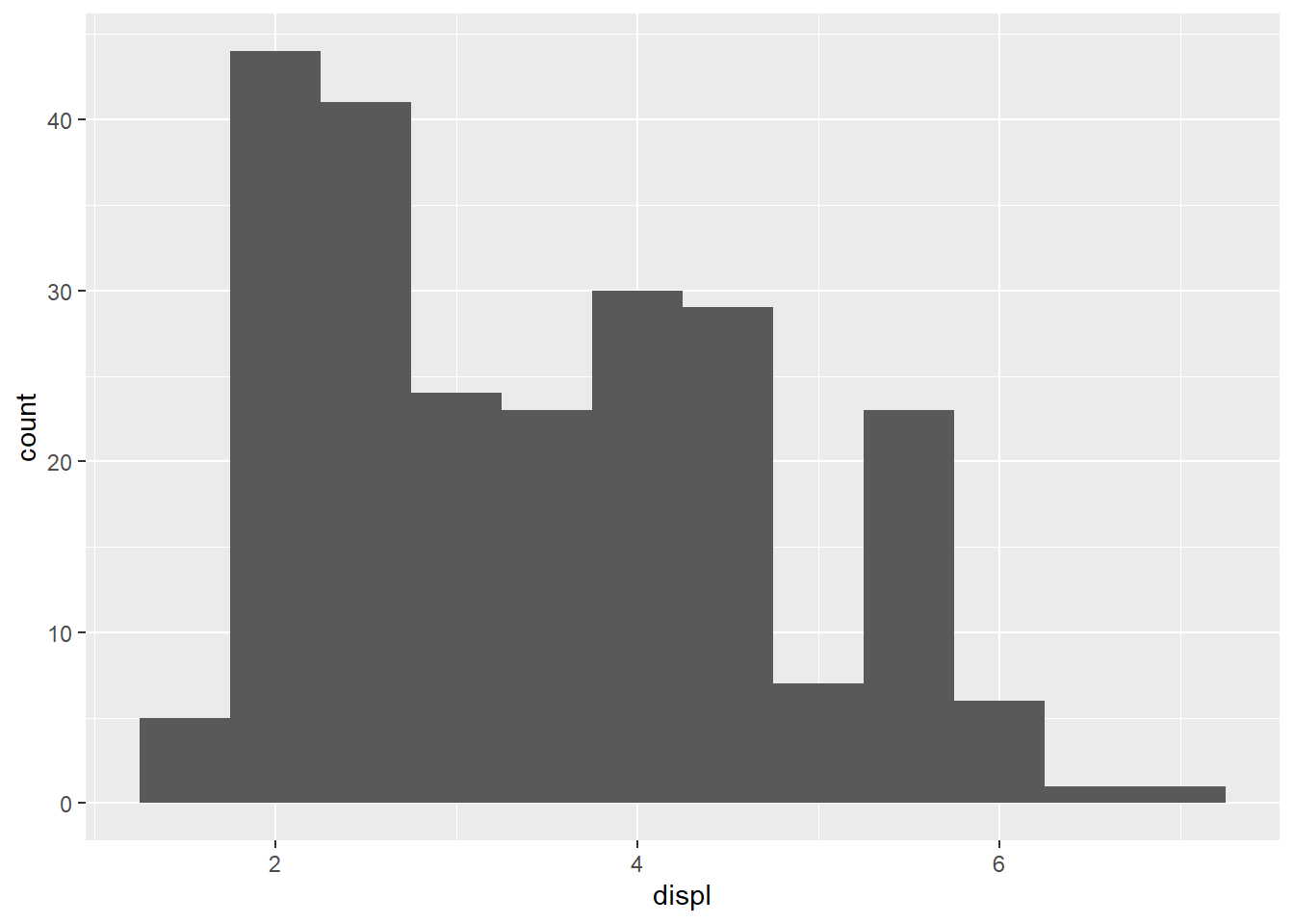

**Figure** 4. Displaying continuous variable with mpg, using histogram.

cut_width function

Display how the histogram was made

For mpg dataset,

mpg %>% 
count(cut_width(displ, 0.5))

# A tibble: 12 × 2
   `cut_width(displ, 0.5)`     n
   <fct>                   <int>
 1 [1.25,1.75]                 5
 2 (1.75,2.25]                44
 3 (2.25,2.75]                41
 4 (2.75,3.25]                24
 5 (3.25,3.75]                23
 6 (3.75,4.25]                30
 7 (4.25,4.75]                29
 8 (4.75,5.25]                 7
 9 (5.25,5.75]                23
10 (5.75,6.25]                 6
11 (6.25,6.75]                 1
12 (6.75,7.25]                 1

Note here that the numbers correspond to the binwidth used in each histogram

Filter function

smaller dataset by filtering. The filter function evaluates a condition inside the bracket.

mpg %>% 
  filter(cty >20)

# A tibble: 45 × 11
   manufacturer model  displ  year   cyl trans     drv     cty   hwy fl    class
   <chr>        <chr>  <dbl> <int> <int> <chr>     <chr> <int> <int> <chr> <chr>
 1 audi         a4       1.8  1999     4 manual(m… f        21    29 p     comp…
 2 audi         a4       2    2008     4 auto(av)  f        21    30 p     comp…
 3 chevrolet    malibu   2.4  2008     4 auto(l4)  f        22    30 r     mids…
 4 honda        civic    1.6  1999     4 manual(m… f        28    33 r     subc…
 5 honda        civic    1.6  1999     4 auto(l4)  f        24    32 r     subc…
 6 honda        civic    1.6  1999     4 manual(m… f        25    32 r     subc…
 7 honda        civic    1.6  1999     4 manual(m… f        23    29 p     subc…
 8 honda        civic    1.6  1999     4 auto(l4)  f        24    32 r     subc…
 9 honda        civic    1.8  2008     4 manual(m… f        26    34 r     subc…
10 honda        civic    1.8  2008     4 auto(l5)  f        25    36 r     subc…
# ℹ 35 more rows

mpg.sub<- mpg %>%
  filter(cty >20)

Plotting a subset of the dataset,

# plotting 
ggplot(data = mpg.sub, mapping = aes(x = cty)) +
  geom_histogram(binwidth = 0.25)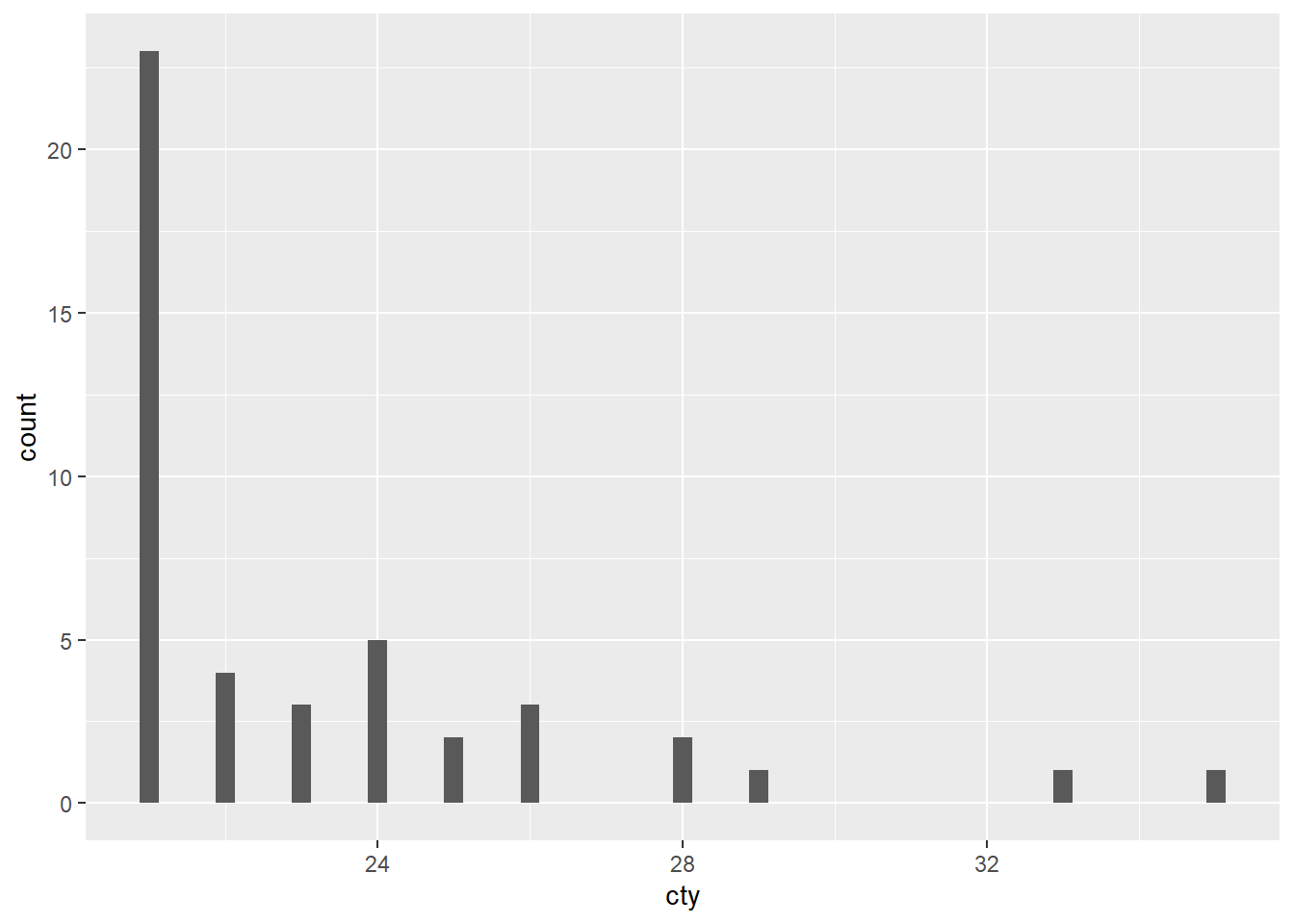

**Figure** 5. Plotting a subset dataset, mpg.

Expanding the x-y limits

# Seeing unusual values
ggplot(mpg) + 
  geom_histogram(mapping = aes(x = displ), binwidth = 0.5)+
  coord_cartesian(ylim = c(0, 50), xlim=c(0,100))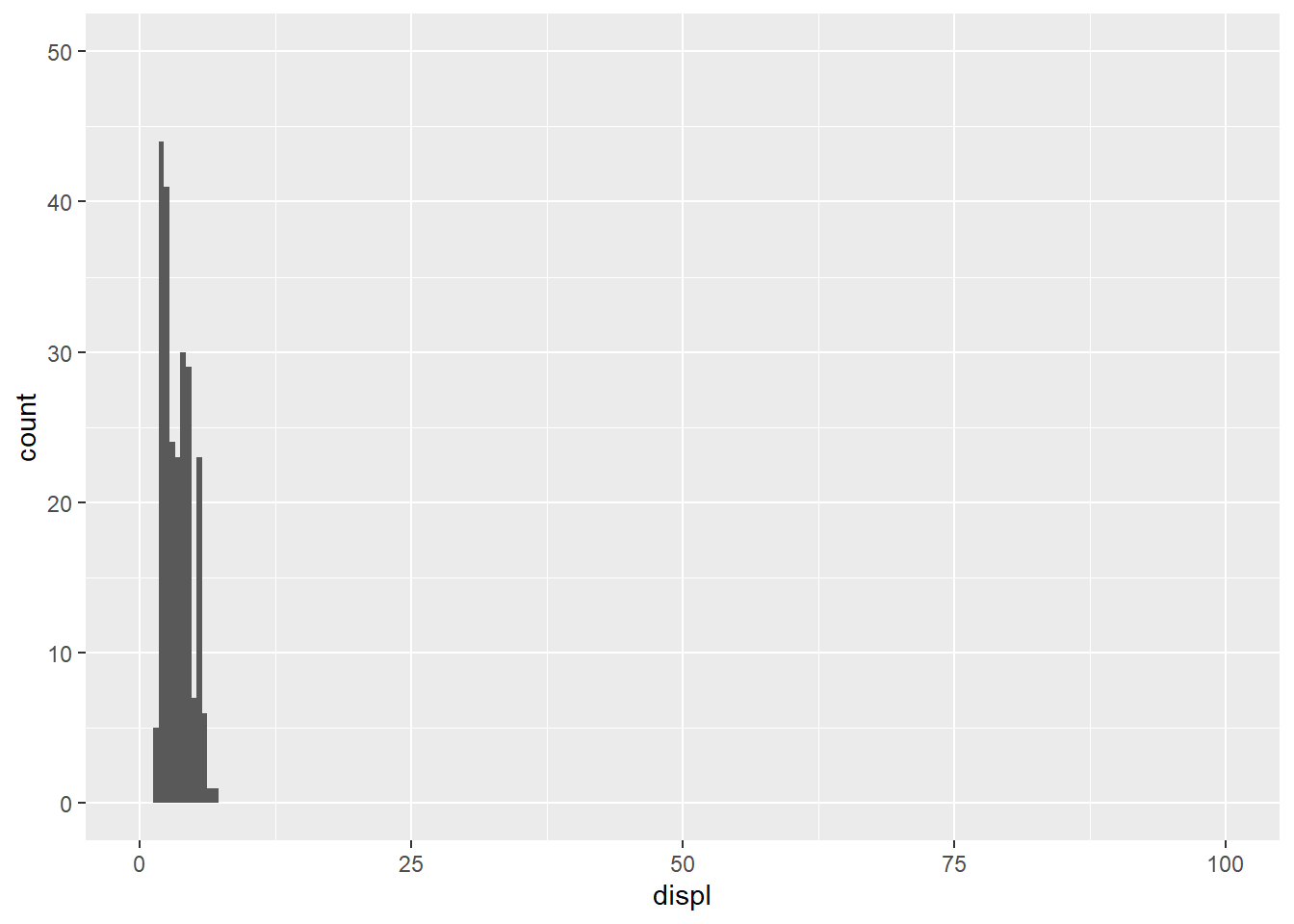

**Figure** 6. Expanding the x-y coordinates,mpg.

Select function

Used for subsetting a dataset, by selecting column names,

mpg.filtered1 <- mpg %>% 
  filter(cty < 10 | cty > 15) %>% 
  select(manufacturer,cty, displ)

mpg.filtered1

# A tibble: 142 × 3
   manufacturer   cty displ
   <chr>        <int> <dbl>
 1 audi            18   1.8
 2 audi            21   1.8
 3 audi            20   2  
 4 audi            21   2  
 5 audi            16   2.8
 6 audi            18   2.8
 7 audi            18   3.1
 8 audi            18   1.8
 9 audi            16   1.8
10 audi            20   2  
# ℹ 132 more rows

Arrange function

Sorts in ascending order by the column name provided,

mpg.filtered2.asc <- mpg %>% 
  filter(cty < 10 | cty > 15) %>% 
  select(manufacturer,cty, displ) %>%
  arrange(cty)

mpg.filtered2.asc

# A tibble: 142 × 3
   manufacturer   cty displ
   <chr>        <int> <dbl>
 1 dodge            9   4.7
 2 dodge            9   4.7
 3 dodge            9   4.7
 4 dodge            9   4.7
 5 jeep             9   4.7
 6 audi            16   2.8
 7 audi            16   1.8
 8 audi            16   4.2
 9 chevrolet       16   5.7
10 chevrolet       16   6.2
# ℹ 132 more rows

Using arrange to sort in descending order, use the function across within arrange.

Note remember you can nest the functions within another function.

mpg.filtered2.dsc <- mpg %>% 
  filter(cty < 10 | cty > 15) %>% 
  select(manufacturer,cty, displ) %>%
  arrange(across(cty,desc))

mpg.filtered2.dsc

# A tibble: 142 × 3
   manufacturer   cty displ
   <chr>        <int> <dbl>
 1 volkswagen      35   1.9
 2 volkswagen      33   1.9
 3 volkswagen      29   1.9
 4 honda           28   1.6
 5 toyota          28   1.8
 6 honda           26   1.8
 7 toyota          26   1.8
 8 toyota          26   1.8
 9 honda           25   1.6
10 honda           25   1.8
# ℹ 132 more rows

Mutate function

Used for adding more columns using a condition. Note here that the notation for

 ifelse(CONDITION, VALUE_IF_TRUE, VALUE_IF_FALSE)

# Mutate - add more columns
mpg.filtered3 <- mpg.filtered2.asc %>% 
  mutate(newcol = ifelse(cty < 10, NA, 0))

mpg.filtered3

# A tibble: 142 × 4
   manufacturer   cty displ newcol
   <chr>        <int> <dbl>  <dbl>
 1 dodge            9   4.7     NA
 2 dodge            9   4.7     NA
 3 dodge            9   4.7     NA
 4 dodge            9   4.7     NA
 5 jeep             9   4.7     NA
 6 audi            16   2.8      0
 7 audi            16   1.8      0
 8 audi            16   4.2      0
 9 chevrolet       16   5.7      0
10 chevrolet       16   6.2      0
# ℹ 132 more rows

You can add multiple columns using mutate function,

mpg.filtered3 <- mpg.filtered2.asc %>% 
  mutate(newcol = ifelse(cty < 10, NA, 0),
         anotherone= cty*5,
         randomcol="weird")

mpg.filtered3

# A tibble: 142 × 6
   manufacturer   cty displ newcol anotherone randomcol
   <chr>        <int> <dbl>  <dbl>      <dbl> <chr>    
 1 dodge            9   4.7     NA         45 weird    
 2 dodge            9   4.7     NA         45 weird    
 3 dodge            9   4.7     NA         45 weird    
 4 dodge            9   4.7     NA         45 weird    
 5 jeep             9   4.7     NA         45 weird    
 6 audi            16   2.8      0         80 weird    
 7 audi            16   1.8      0         80 weird    
 8 audi            16   4.2      0         80 weird    
 9 chevrolet       16   5.7      0         80 weird    
10 chevrolet       16   6.2      0         80 weird    
# ℹ 132 more rows

Boxplot

Using function geom_boxplot to look at trends in data,

# Boxplot
ggplot(data = mpg, mapping = aes(x = manufacturer, y = hwy)) +
  geom_boxplot()+
  xlab("highway miles")+
  ylab("manufacturer")

Reorder function

Using function reorder to see a clear trend.
Note that reorder is a special case of the function factor.
The factor function is in base R and is used for ordering vector data.

# Easy to see trend
ggplot(data = mpg) +
  geom_boxplot(mapping = aes(x = reorder(manufacturer, hwy, FUN = median), y = hwy))+
  xlab("highway miles")+
  ylab("manufacturer")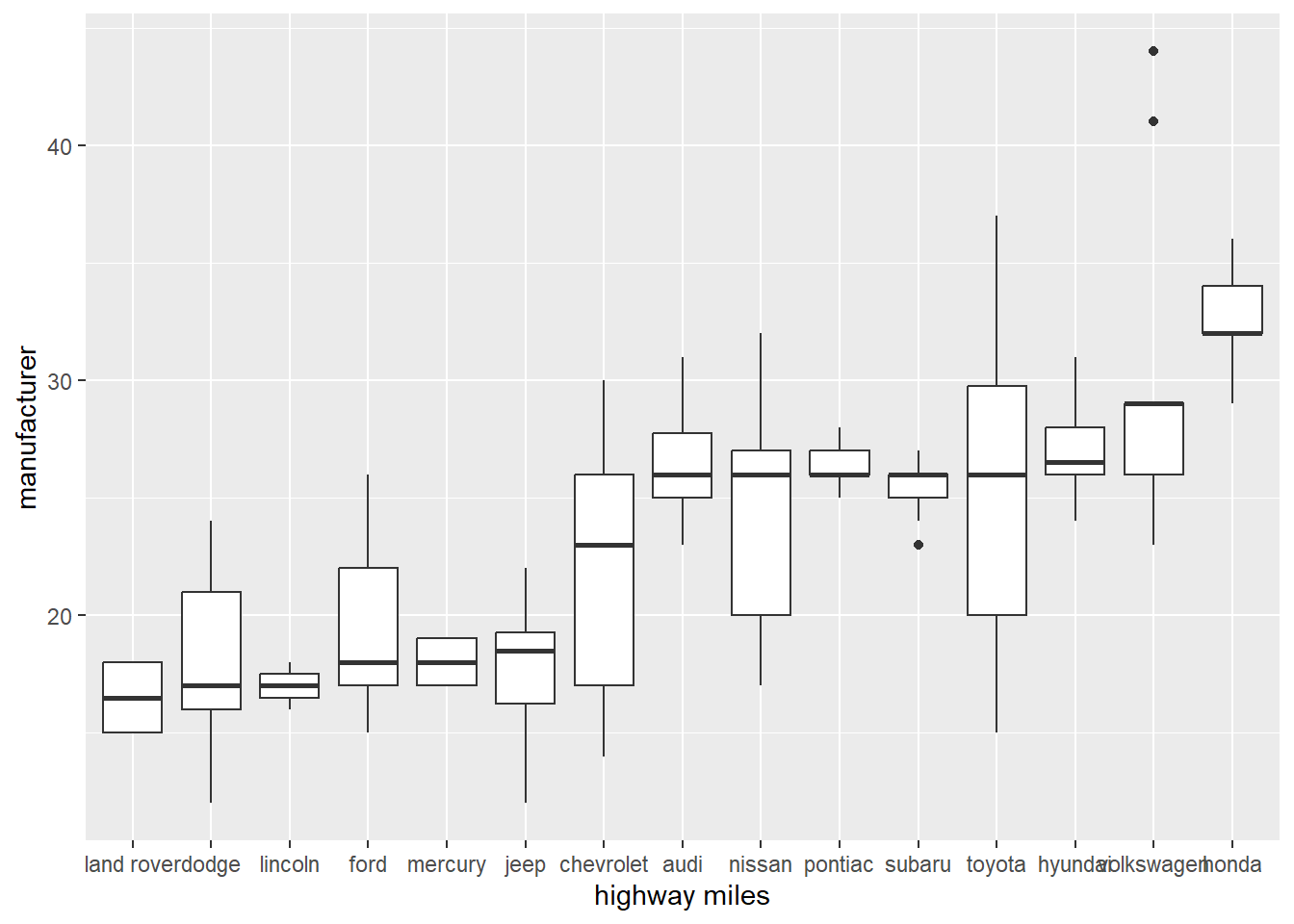

**Figure** 8. Clear trend using reorder function.

Flip the coordinates

# Flip coordinates
ggplot(data = mpg) +
  geom_boxplot(mapping = aes(x = reorder(manufacturer, hwy, FUN = median), y = hwy))+
  coord_flip()+
  xlab("highway miles")+
  ylab("manufacturer")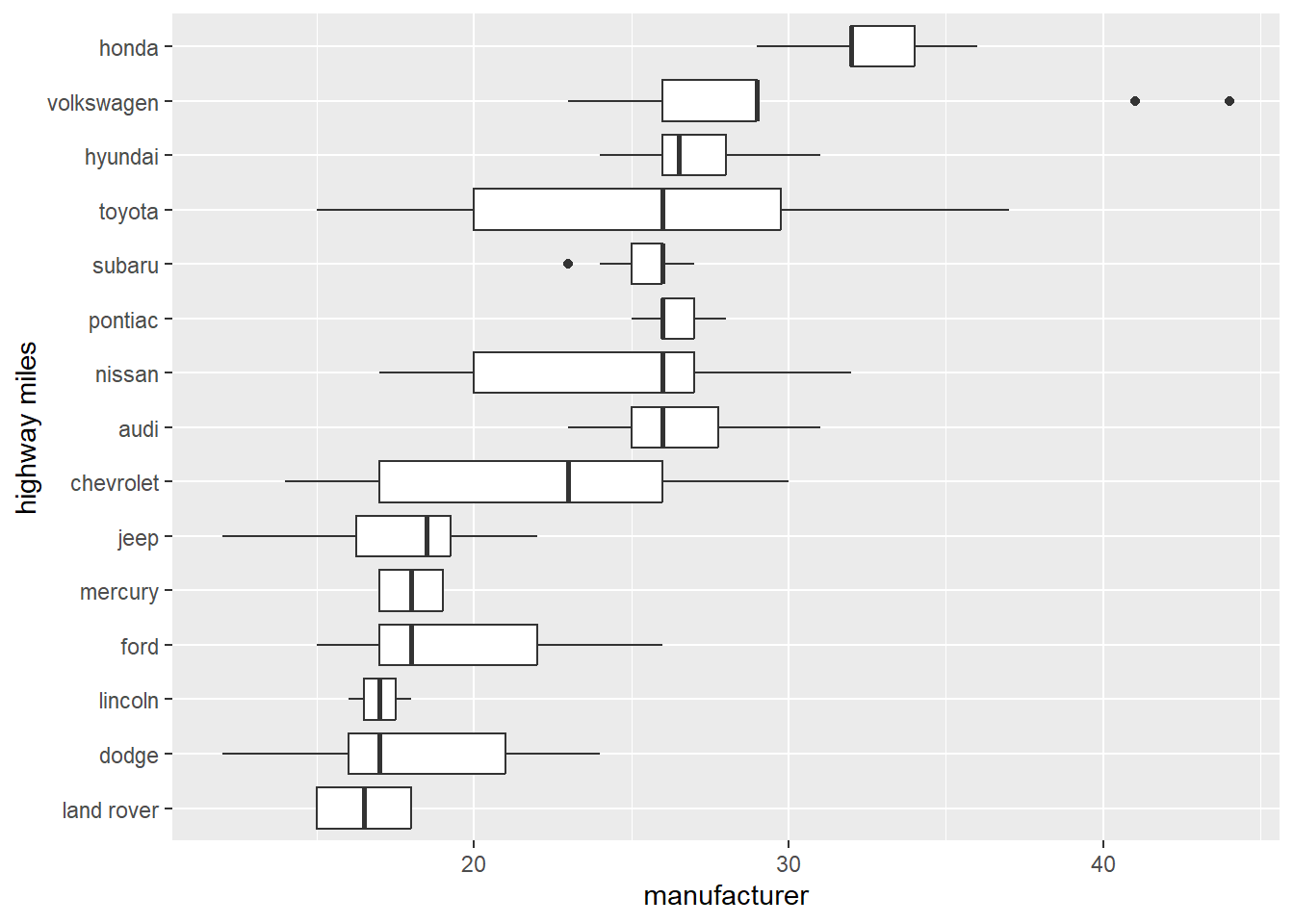

Scatterplot of the data

Geom point is used for looking at a scatterplot,

# Scatterplot
ggplot(data = mpg) +
  geom_point(mapping = aes(x = manufacturer, y = hwy))+
   xlab("highway miles")+
   ylab("manufacturer")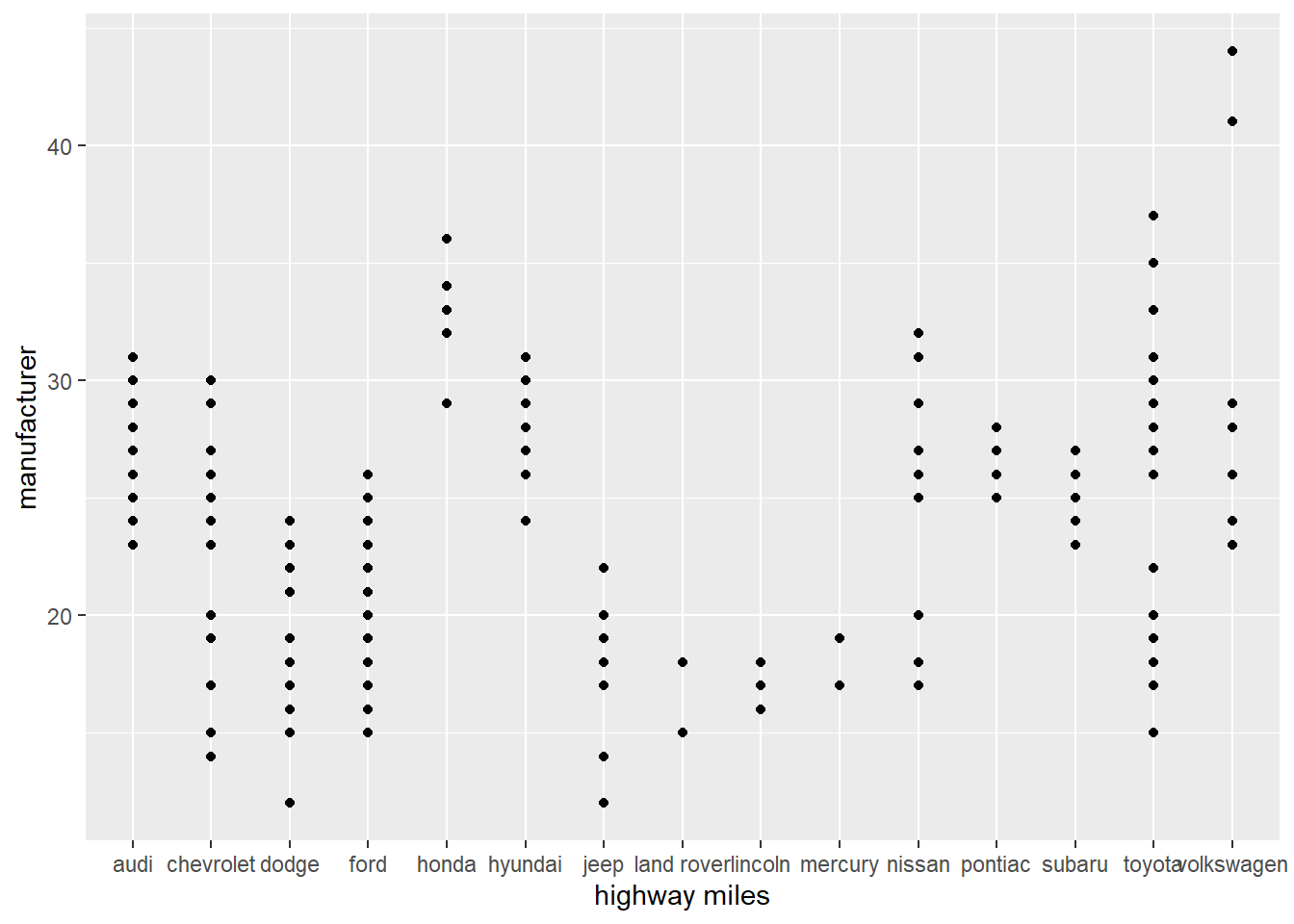

**Figure** 10. Scatterplot of the data,mpg.

Finding patterns in data through modelling

Refine the questions based on what you learn and repeat the process. Let’s ask a new question.

How highway miles are varying with city miles?

# How highway miles are varying with city miles
ggplot(data = mpg)+ 
  geom_point(mapping = aes(x = hwy,y=cty))+
   xlab("highway miles")+
   ylab("city miles")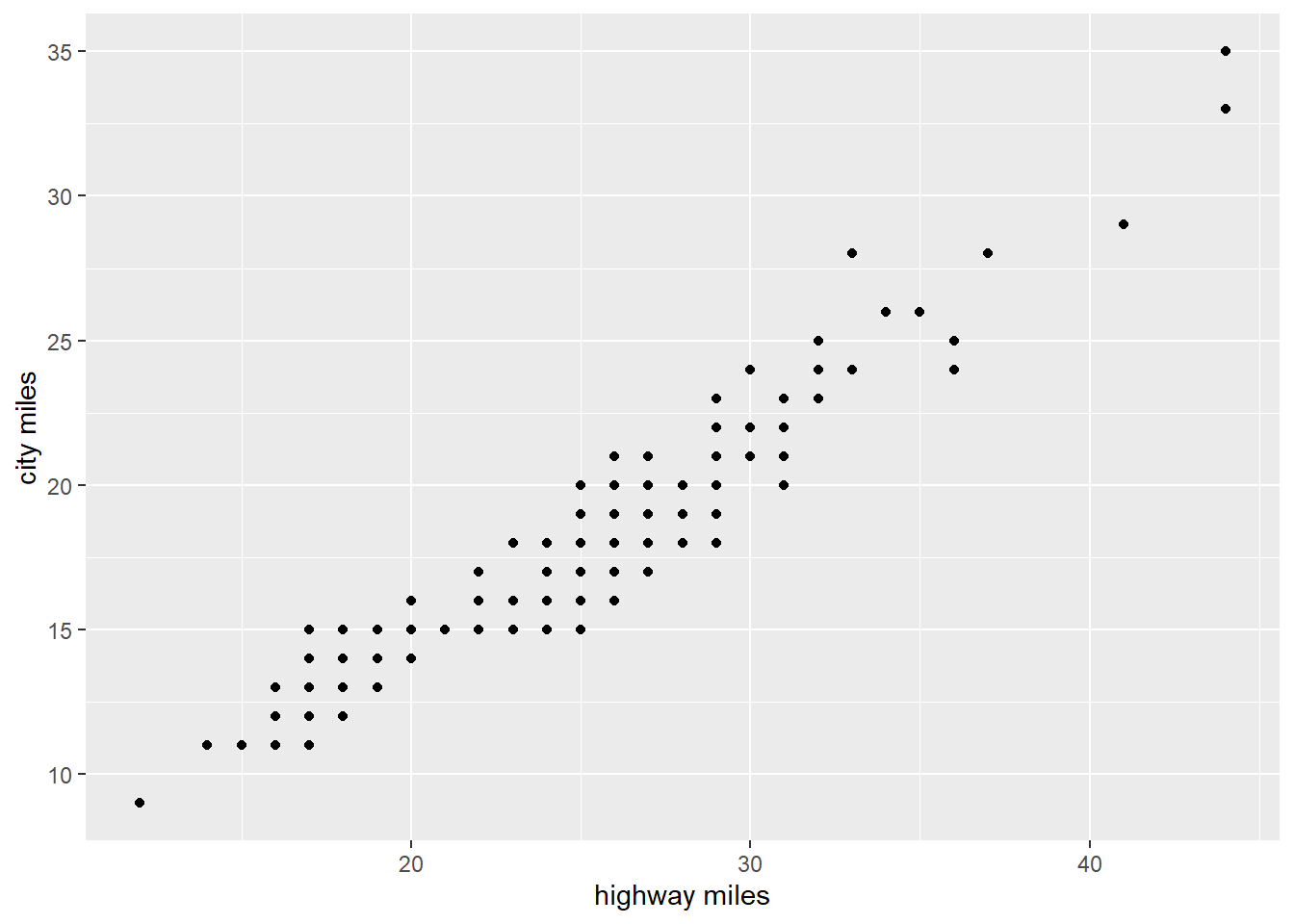

**Figure** 11. Scatterplot of city miles v/s highway miles.

Linear regression

Are highway miles linearly related with city miles?

Defining a linear model

lm(hwy~cty,data = mpg)


Call:
lm(formula = hwy ~ cty, data = mpg)

Coefficients:
(Intercept)          cty  
      0.892        1.337

model1<-lm(hwy~cty,data = mpg)
summary(model1)


Call:
lm(formula = hwy ~ cty, data = mpg)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.3408 -1.2790  0.0214  1.0338  4.0461 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.89204    0.46895   1.902   0.0584 .  
cty          1.33746    0.02697  49.585   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.752 on 232 degrees of freedom
Multiple R-squared:  0.9138,    Adjusted R-squared:  0.9134 
F-statistic:  2459 on 1 and 232 DF,  p-value: < 2.2e-16

plot(model1)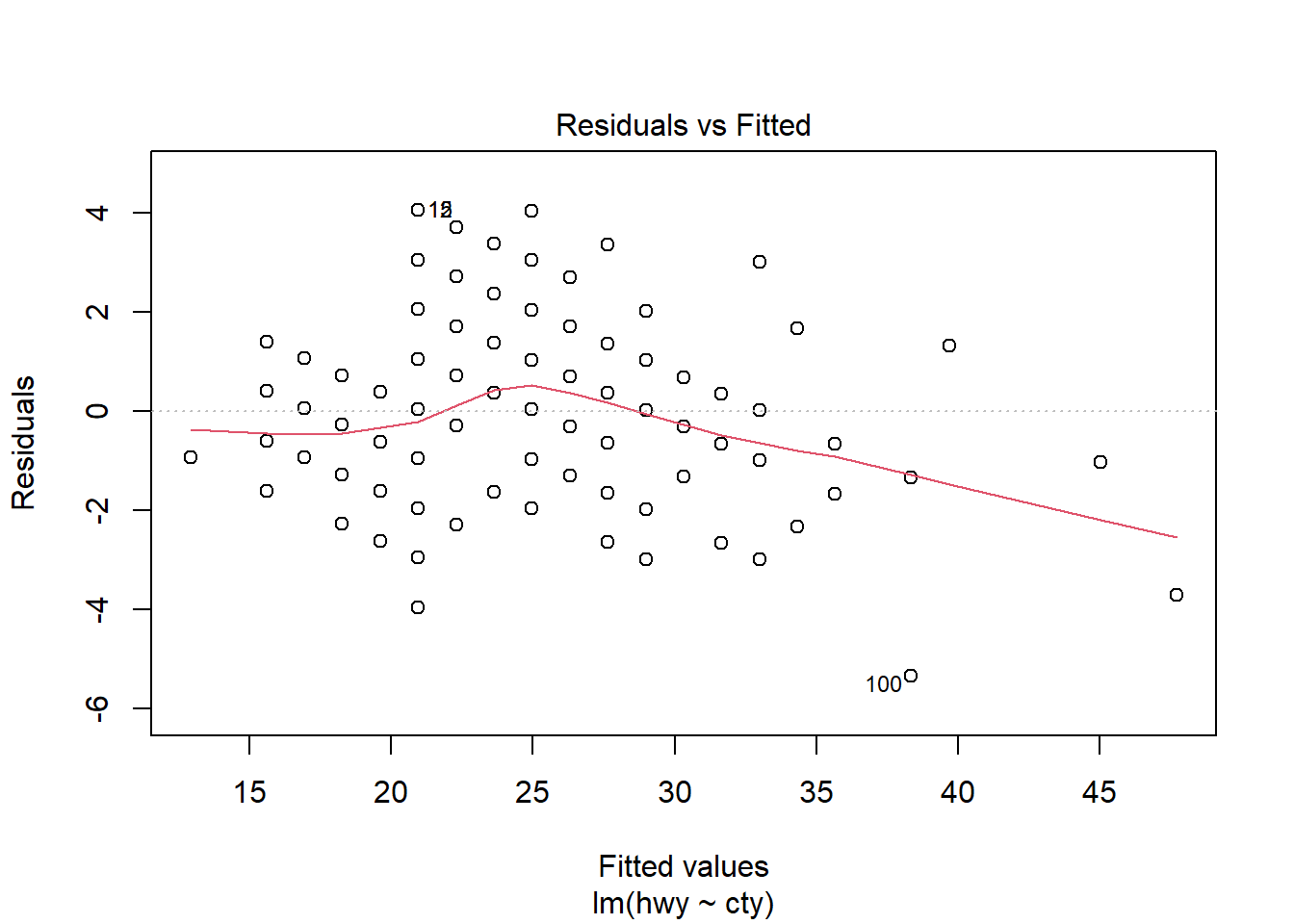

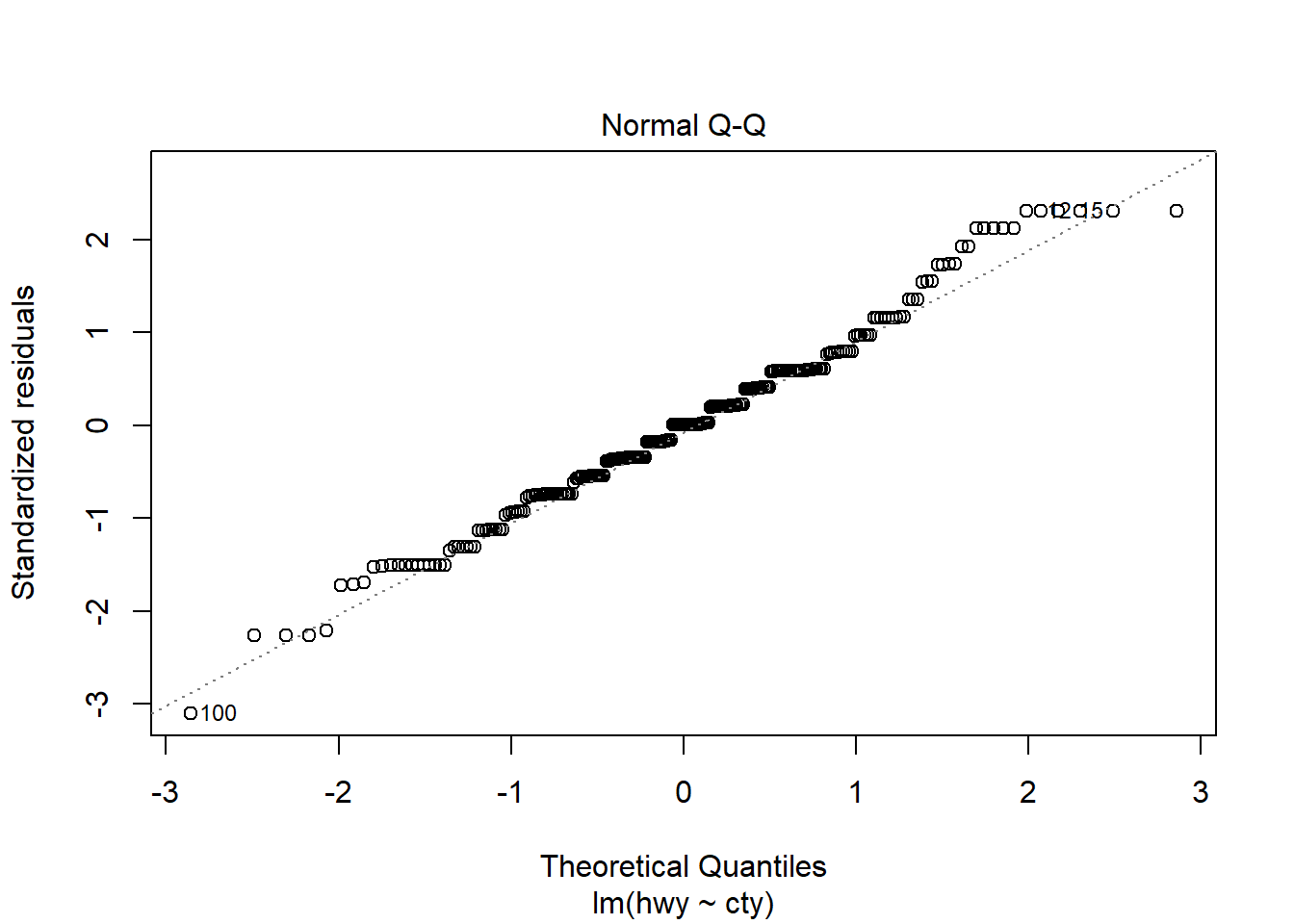
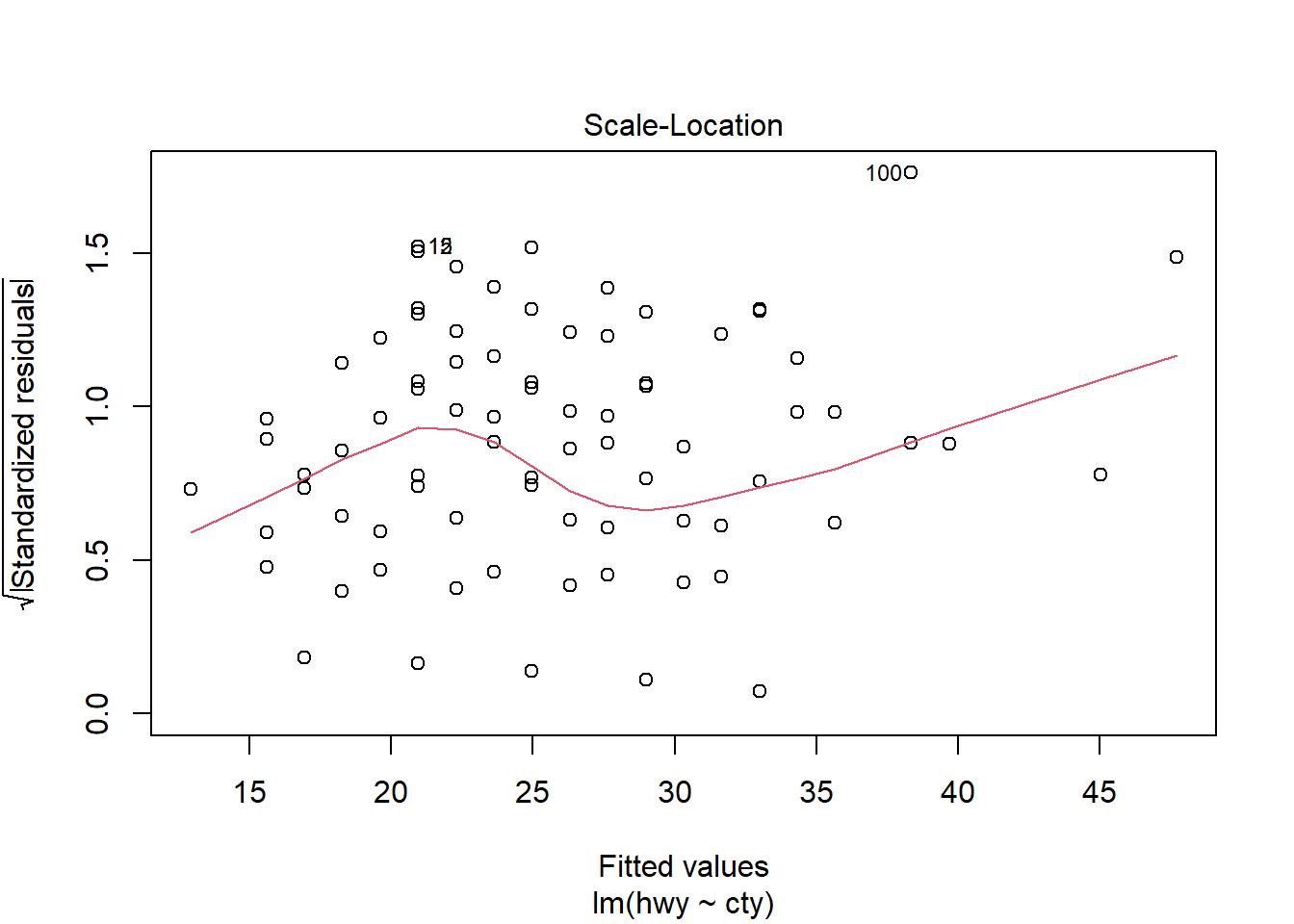
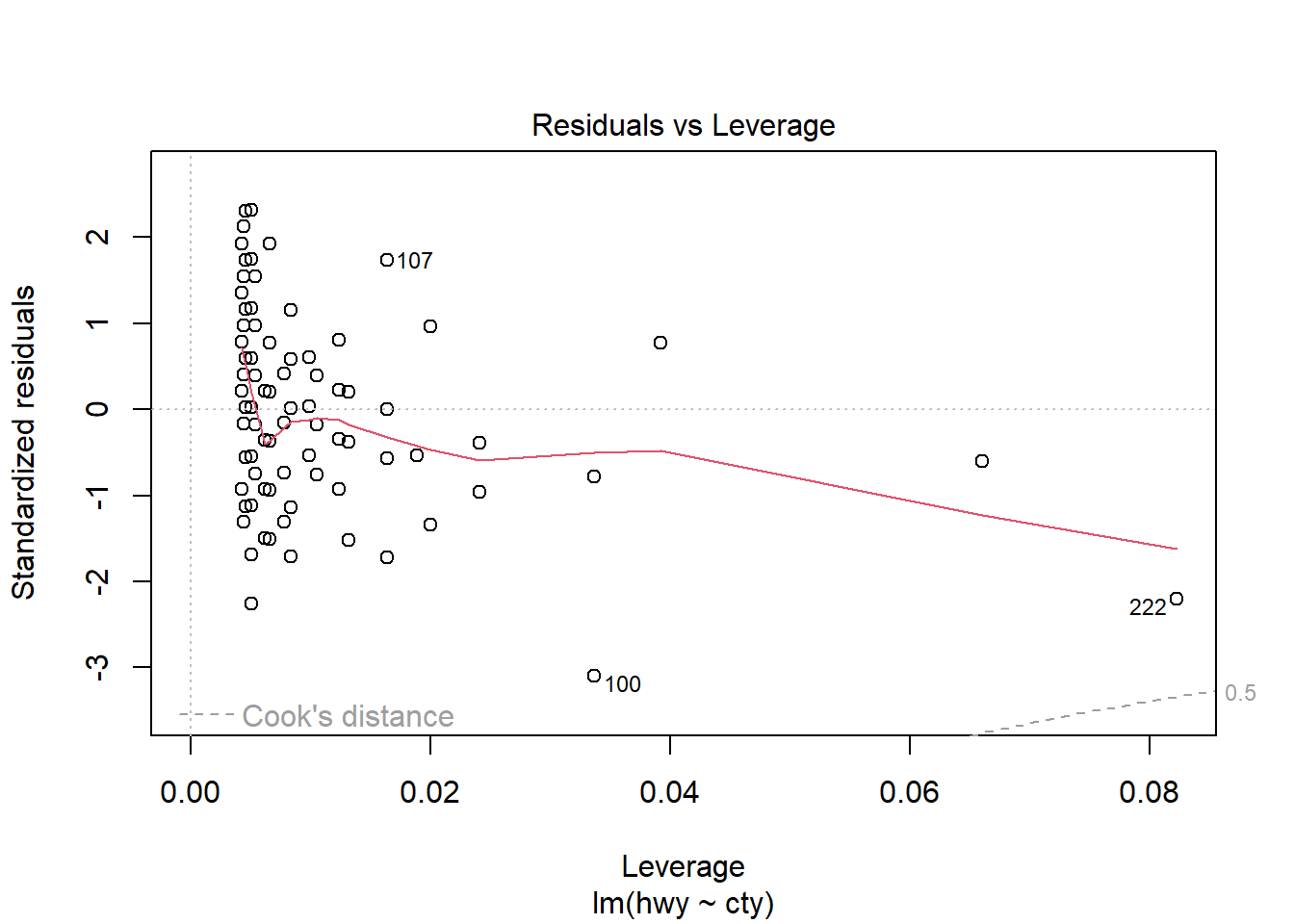
# Other useful functions
coefficients(model1) # model coefficients

(Intercept)         cty 
  0.8920411   1.3374556

confint(model1, level=0.95) # Confidence Intervals for model parameters

                  2.5 %   97.5 %
(Intercept) -0.03189534 1.815978
cty          1.28431197 1.390599

residuals(model1) # residuals values

           1            2            3            4            5            6 
 4.033757915  0.021391084  3.358846694  1.021391084  3.708669135  1.033757915 
           7            8            9           10           11           12 
 2.033757915  1.033757915  2.708669135  0.358846694  0.696302304  4.046124746 
          13           14           15           16           17           18 
 1.371213525  1.371213525  4.046124746  3.046124746  1.371213525  0.708669135 
          19           20           21           22           23           24 
 0.383580356 -0.604052813  0.383580356 -1.278964034  0.058491577  3.708669135 
          25           26           27           28           29           30 
 2.046124746  3.708669135  4.046124746  3.046124746 -0.616419644 -1.604052813 
          31           32           33           34           35           36 
-0.604052813 -2.616419644  0.696302304 -0.316064527  1.033757915  4.033757915 
          37           38           39           40           41           42 
 2.371213525 -0.966242085  0.371213525 -0.291330865 -0.291330865  0.371213525 
          43           44           45           46           47           48 
 0.371213525  1.395947187  1.046124746  0.046124746  0.708669135  0.708669135 
          49           50           51           52           53           54 
-1.953875254 -1.616419644 -1.278964034 -2.616419644 -0.616419644 -0.616419644 
          55           56           57           58           59           60 
-0.929141592  1.395947187 -0.604052813 -1.278964034 -1.278964034 -0.929141592 
          61           62           63           64           65           66 
-1.278964034  0.395947187 -0.278964034 -0.604052813 -0.941508423 -0.929141592 
          67           68           69           70           71           72 
-1.278964034 -1.278964034 -0.941508423 -0.929141592 -0.604052813  0.395947187 
          73           74           75           76           77           78 
-1.278964034 -0.604052813  1.395947187  1.395947187  1.058491577 -2.616419644 
          79           80           81           82           83           84 
-1.953875254 -2.616419644  0.721035966  0.721035966 -1.278964034 -2.616419644 
          85           86           87           88           89           90 
-2.616419644 -2.278964034 -2.278964034 -1.278964034 -0.604052813 -1.278964034 
          91           92           93           94           95           96 
 1.033757915  0.033757915  2.371213525  1.708669135  0.046124746  1.046124746 
          97           98           99          100          101          102 
 2.046124746  1.046124746  0.383580356 -5.340798189 -0.990975747 -2.328431358 
         103          104          105          106          107          108 
-2.653520137 -0.990975747 -1.665886968  1.671568642  3.009024253  0.021391084 
         109          110          111          112          113          114 
 1.033757915  2.033757915  1.021391084  2.021391084  1.033757915  1.033757915 
         115          116          117          118          119          120 
 1.696302304 -0.303697696  2.696302304  0.358846694 -0.641153306  0.371213525 
         121          122          123          124          125          126 
 1.708669135  0.371213525 -1.628786475 -1.953875254 -0.953875254 -2.616419644 
         127          128          129          130          131          132 
-0.929141592 -0.616419644 -0.278964034 -1.604052813 -0.604052813  1.058491577 
         133          134          135          136          137          138 
 1.058491577 -0.604052813  1.395947187  0.395947187  1.058491577 -2.616419644 
         139          140          141          142          143          144 
 0.721035966  0.721035966 -1.278964034  0.021391084  0.696302304 -0.653520137 
         145          146          147          148          149          150 
 0.346479863  0.696302304 -0.303697696  1.033757915 -1.303697696 -1.303697696 
         151          152          153          154          155          156 
-2.616419644 -3.953875254  0.383580356  1.058491577  1.033757915  3.708669135 
         157          158          159          160          161          162 
 3.371213525  3.033757915  2.708669135  0.033757915 -0.966242085 -0.641153306 
         163          164          165          166          167          168 
-1.303697696 -1.641153306 -1.966242085 -2.978608916 -0.303697696 -0.303697696 
         169          170          171          172          173          174 
-0.303697696 -2.641153306 -0.641153306 -1.303697696 -0.641153306 -0.953875254 
         175          176          177          178          179          180 
-2.291330865 -1.953875254 -3.953875254 -2.291330865 -2.616419644  0.021391084 
         181          182          183          184          185          186 
-1.978608916  2.021391084  2.021391084  1.033757915  1.033757915  1.696302304 
         187          188          189          190          191          192 
-1.978608916  0.021391084  2.021391084  0.683935473  1.033757915  1.033757915 
         193          194          195          196          197          198 
 2.033757915 -2.990975747  0.009024253 -0.665886968 -1.340798189 -0.665886968 
         199          200          201          202          203          204 
-0.604052813 -0.278964034 -0.953875254 -2.291330865 -1.628786475 -3.953875254 
         205          206          207          208          209          210 
-1.953875254 -2.953875254 -2.291330865  0.021391084 -0.303697696  0.021391084 
         211          212          213          214          215          216 
-1.316064527  0.371213525 -1.028076240  0.021391084 -0.303697696 -1.316064527 
         217          218          219          220          221          222 
 0.021391084  0.021391084  0.021391084  0.708669135  0.371213525 -3.702987461 
         223          224          225          226          227          228 
 1.321746201  0.021391084 -0.303697696  0.358846694  1.358846694  0.021391084 
         229          230          231          232          233          234 
 4.033757915  1.696302304  0.021391084  3.708669135  1.033757915  2.371213525

plot(residuals(model1)) # residuals plots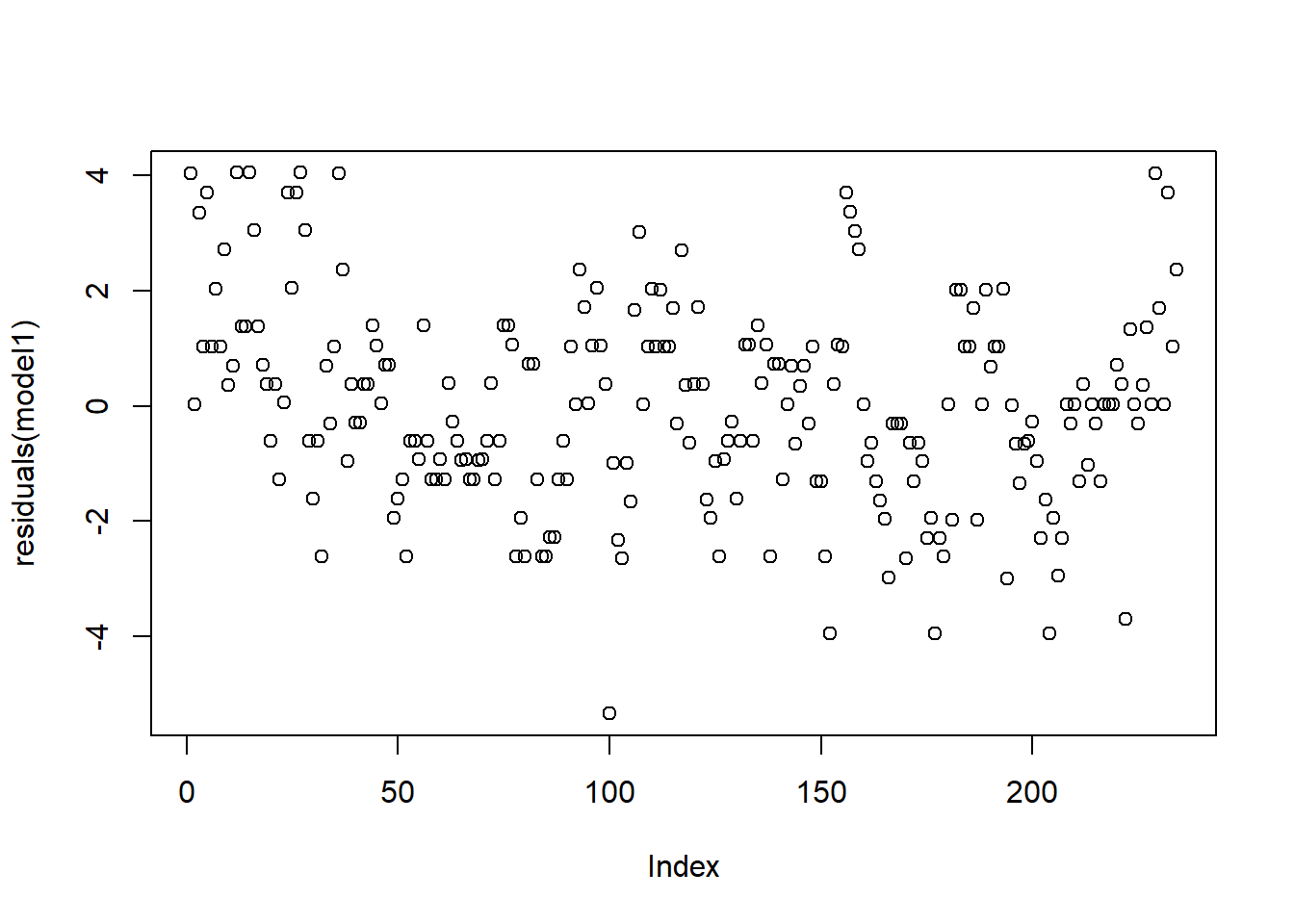

Using add_residual function within tidyverse

# Using ggplot2 and add_residual function
mpg.model1 <- mpg %>% 
  add_residuals(model1) %>% 
  mutate(resid = exp(resid))

ggplot(data = mpg.model1) + 
  geom_point(mapping = aes(x = hwy, y = resid))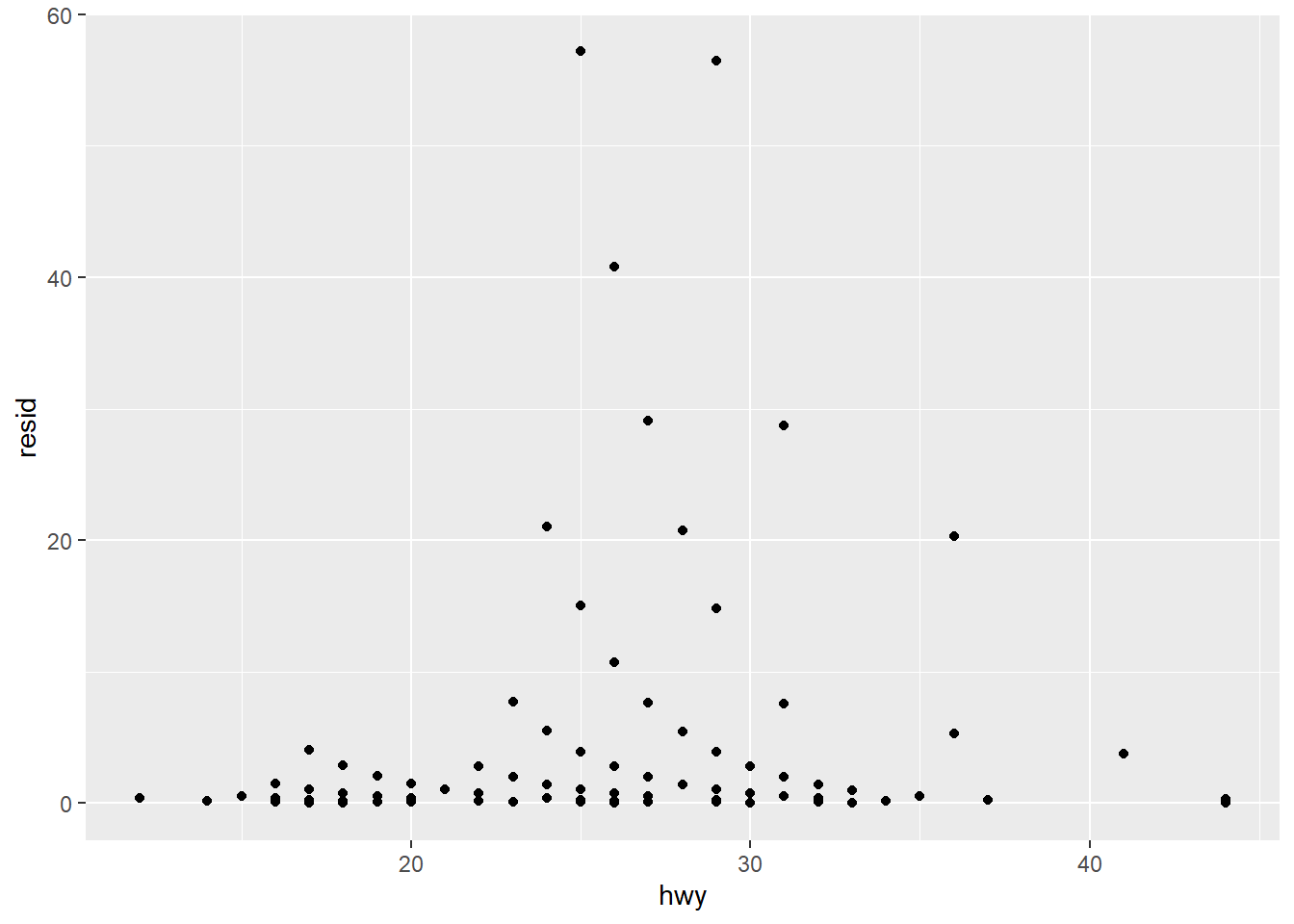

**Figure** 12. Adding residuals to ggplot, mpg.

Is there a logarithmic relationship?

lm(log(hwy)~cty,data = mpg)


Call:
lm(formula = log(hwy) ~ cty, data = mpg)

Coefficients:
(Intercept)          cty  
    2.16112      0.05697

Finding correlation

cor() : computes the correlation coefficient
cor.test() : test for association/correlation between paired samples. It returns both the correlation coefficient and the significance level(or p-value) of the correlation.

# Default method: Pearson
cor(mpg$cty, mpg$hwy)

[1] 0.9559159

cor.test(mpg$cty, mpg$hwy, method="pearson")


    Pearson's product-moment correlation

data:  mpg$cty and mpg$hwy
t = 49.585, df = 232, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.9433129 0.9657663
sample estimates:
      cor 
0.9559159

# Save into a vector
cor.result<-cor.test(mpg$cty, mpg$hwy, method="pearson")

t is the t-test statistic value;
df is the degrees of freedom;
p-value is the significance level of the t-test;
conf.int is the confidence interval of the correlation coefficient at 95%;
sample estimates is the correlation coefficient(Cor.coeff)

# Extract the p.value
cor.result$p.value

[1] 1.868307e-125

# Extract the correlation coefficient
cor.result$estimate

      cor 
0.9559159

T-test

t.test(mpg$cty, mpg$hwy) # here both the variable are numeric


    Welch Two Sample t-test

data:  mpg$cty and mpg$hwy
t = -13.755, df = 421.79, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -7.521683 -5.640710
sample estimates:
mean of x mean of y 
 16.85897  23.44017

# paired t-test
t.test(mpg$cty,mpg$hwy,paired=TRUE) # both the variable are numeric


    Paired t-test

data:  mpg$cty and mpg$hwy
t = -44.492, df = 233, p-value < 2.2e-16
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -6.872628 -6.289765
sample estimates:
mean difference 
      -6.581197

You can use the var.equal = TRUE option to specify equal variances and a pooled variance estimate.
You can use the alternative=“less” or alternative=“greater” option to specify a one tailed test.

Simulated dataset using probability distribution

# Creating simulated data to work
set.seed(5)

xvar <- 1:20 + rnorm(20,sd=3)
zvar <- (1:20)/4 + rnorm(20,sd=2)
yvar <- -2*xvar + xvar*zvar/5 + 3 + rnorm(20,sd=4)

# Make a data frame 
mydat <- data.frame(x=xvar, y=yvar, z=zvar)

# first 6 rows
head(mydat)

           x          y         z
1 -1.5225664  11.620810 2.0510239
2  6.1530780  -9.582383 2.3837388
3 -0.7664756   3.669601 3.6859238
4  4.2104283   4.194208 2.4135222
5 10.1343226 -13.241300 2.8880179
6  4.1912761  -2.368301 0.9130363

T-test

# independent 2-group t-test
#t.test(y~x) # where y is numeric and x is a binary factor

# independent 2-group t-test
t.test(yvar,xvar) # where y1 and y2 are numeric


    Welch Two Sample t-test

data:  yvar and xvar
t = -7.1706, df = 30.697, p-value = 4.899e-08
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -23.70438 -13.20283
sample estimates:
mean of x mean of y 
-8.795275  9.658327

# paired t-test
t.test(yvar,xvar,paired=TRUE) # where yvar,xvar are numeric


    Paired t-test

data:  yvar and xvar
t = -5.4883, df = 19, p-value = 2.703e-05
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -25.49104 -11.41616
sample estimates:
mean difference 
       -18.4536

Correlation

Pearson’s

# Correlation between xvar and yvar 
# Default method: Pearson
cor(mydat$x, mydat$y)

[1] -0.8098878

cor.test(mydat$x, mydat$y, method="pearson")


    Pearson's product-moment correlation

data:  mydat$x and mydat$y
t = -5.8577, df = 18, p-value = 1.51e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.9219786 -0.5725725
sample estimates:
       cor 
-0.8098878

# Save into a vector
cor.result<-cor.test(mydat$x, mydat$y, method="pearson")

# Extract the p.value
cor.result$p.value

[1] 1.510141e-05

# Extract the correlation coefficient
cor.result$estimate

       cor 
-0.8098878

Spearman’s

# Spearman's correlation
cor(mydat$x, mydat$y, method="spearman")

[1] -0.7804511

cor.test(mydat$x, mydat$y, method="spearman")


    Spearman's rank correlation rho

data:  mydat$x and mydat$y
S = 2368, p-value = 7.156e-05
alternative hypothesis: true rho is not equal to 0
sample estimates:
       rho 
-0.7804511

Kendall’s

# Kendall's correlation
cor(mydat$x, mydat$y, method="kendall")

[1] -0.6210526

cor.test(mydat$x, mydat$y, method="kendall")


    Kendall's rank correlation tau

data:  mydat$x and mydat$y
T = 36, p-value = 5.177e-05
alternative hypothesis: true tau is not equal to 0
sample estimates:
       tau 
-0.6210526